The history of computers is often told as a history of objects, from the abacus to the Babbage engine up through the code-breaking machines of World War II. In fact, it is better understood as a history of ideas, mainly ideas that emerged from mathematical logic, an obscure and cult-like discipline that first developed in the 19th century. Mathematical logic was pioneered by philosopher-mathematicians, most notably George Boole and Gottlob Frege, who were themselves inspired by Leibniz’s dream of a universal “concept language,” and the ancient logical system of Aristotle.
Mathematical logic was initially considered a hopelessly abstract subject with no conceivable applications. As one computer scientist commented: “If, in 1901, a talented and sympathetic outsider had been called upon to survey the sciences and name the branch which would be least fruitful in [the] century ahead, his choice might well have settled upon mathematical logic.” And yet, it would provide the foundation for a field that would have more impact on the modern world than any other.
The evolution of computer science from mathematical logic culminated in the 1930s, with two landmark papers: Claude Shannon’s “A Symbolic Analysis of Switching and Relay Circuits,” and Alan Turing’s “On Computable Numbers, With an Application to the Entscheidungsproblem.” In the history of computer science, Shannon and Turing are towering figures, but the importance of the philosophers and logicians who preceded them is frequently overlooked.
A well-known history of computer science describes Shannon’s paper as “possibly the most important, and also the most noted, master’s thesis of the century.” Shannon wrote it as an electrical engineering student at MIT. His adviser, Vannevar Bush, built a prototype computer known as the Differential Analyzerthat could rapidly calculate differential equations. The device was mostly mechanical, with subsystems controlled by electrical relays, which were organized in an ad hoc manner as there was not yet a systematic theory underlying circuit design. Shannon’s thesis topic came about when Bush recommended he try to discover such a theory.
“Mathematics may be defined as the subject in which we never know what we are talking about.”
Shannon’s paper is in many ways a typical electrical-engineering paper, filled with equations and diagrams of electrical circuits. What is unusual is that the primary reference was a 90-year-old work of mathematical philosophy, George Boole’s The Laws of Thought.
Today, Boole’s name is well known to computer scientists (many programming languages have a basic data type called a Boolean), but in 1938 he was rarely read outside of philosophy departments. Shannon himself encountered Boole’s work in an undergraduate philosophy class. “It just happened that no one else was familiar with both fields at the same time,” he commented later.
Boole is often described as a mathematician, but he saw himself as a philosopher, following in the footsteps of Aristotle. The Laws of Thought begins with a description of his goals, to investigate the fundamental laws of the operation of the human mind:
The design of the following treatise is to investigate the fundamental laws of those operations of the mind by which reasoning is performed; to give expression to them in the symbolical language of a Calculus, and upon this foundation to establish the science of Logic … and, finally, to collect … some probable intimations concerning the nature and constitution of the human mind.
He then pays tribute to Aristotle, the inventor of logic, and the primary influence on his own work:
In its ancient and scholastic form, indeed, the subject of Logic stands almost exclusively associated with the great name of Aristotle. As it was presented to ancient Greece in the partly technical, partly metaphysical disquisitions of The Organon, such, with scarcely any essential change, it has continued to the present day.
Trying to improve on the logical work of Aristotle was an intellectually daring move. Aristotle’s logic, presented in his six-part book The Organon, occupied a central place in the scholarly canon for more than 2,000 years. It was widely believed that Aristotle had written almost all there was to say on the topic. The great philosopher Immanuel Kant commented that, since Aristotle, logic had been “unable to take a single step forward, and therefore seems to all appearance to be finished and complete.”
Aristotle’s central observation was that arguments were valid or not based on their logical structure, independent of the non-logical words involved. The most famous argument schema he discussed is known as the syllogism:
- All men are mortal.
- Socrates is a man.
- Therefore, Socrates is mortal.
You can replace “Socrates” with any other object, and “mortal” with any other predicate, and the argument remains valid. The validity of the argument is determined solely by the logical structure. The logical words — “all,” “is,” are,” and “therefore” – are doing all the work.
Aristotle also defined a set of basic axioms from which he derived the rest of his logical system:
- An object is what it is (Law of Identity)
- No statement can be both true and false (Law of Non-contradiction)
- Every statement is either true or false (Law of the Excluded Middle)
These axioms weren’t meant to describe how people actually think (that would be the realm of psychology), but how an idealized, perfectly rational person ought to think.
Aristotle’s axiomatic method influenced an even more famous book, Euclid’s Elements, which is estimated to be second only to the Bible in the number of editions printed.

A fragment of the Elements (Wikimedia Commons)
Although ostensibly about geometry, the Elements became a standard textbook for teaching rigorous deductive reasoning. (Abraham Lincoln once said that he learned sound legal argumentation from studying Euclid.) In Euclid’s system, geometric ideas were represented as spatial diagrams. Geometry continued to be practiced this way until René Descartes, in the 1630s, showed that geometry could instead be represented as formulas. His Discourse on Method was the first mathematics text in the West to popularize what is now standard algebraic notation — x, y, z for variables, a, b, c for known quantities, and so on.
Descartes’s algebra allowed mathematicians to move beyond spatial intuitions to manipulate symbols using precisely defined formal rules. This shifted the dominant mode of mathematics from diagrams to formulas, leading to, among other things, the development of calculus, invented roughly 30 years after Descartes by, independently, Isaac Newton and Gottfried Leibniz.
Boole’s goal was to do for Aristotelean logic what Descartes had done for Euclidean geometry: free it from the limits of human intuition by giving it a precise algebraic notation. To give a simple example, when Aristotle wrote:
All men are mortal.
Boole replaced the words “men” and “mortal” with variables, and the logical words “all” and “are” with arithmetical operators:
x = x * y
Which could be interpreted as “Everything in the set x is also in the set y.”
The Laws of Thought created a new scholarly field — mathematical logic — which in the following years became one of the most active areas of research for mathematicians and philosophers. Bertrand Russell called the Laws of Thought “the work in which pure mathematics was discovered.”
Shannon’s insight was that Boole’s system could be mapped directly onto electrical circuits. At the time, electrical circuits had no systematic theory governing their design. Shannon realized that the right theory would be “exactly analogous to the calculus of propositions used in the symbolic study of logic.”
He showed the correspondence between electrical circuits and Boolean operations in a simple chart:

Shannon’s mapping from electrical circuits to symbolic logic (University of Virginia)
This correspondence allowed computer scientists to import decades of work in logic and mathematics by Boole and subsequent logicians. In the second half of his paper, Shannon showed how Boolean logic could be used to create a circuit for adding two binary digits.
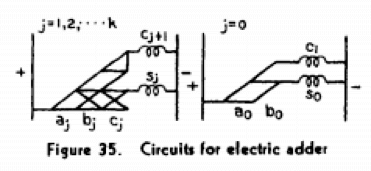
Shannon’s adder circuit (University of Virginia)
By stringing these adder circuits together, arbitrarily complex arithmetical operations could be constructed. These circuits would become the basic building blocks of what are now known as arithmetical logic units, a key component in modern computers.
Another way to characterize Shannon’s achievement is that he was first to distinguish between the logical and the physical layer of computers. (This distinction has become so fundamental to computer science that it might seem surprising to modern readers how insightful it was at the time — a reminder of the adage that “the philosophy of one century is the common sense of the next.”)
Since Shannon’s paper, a vast amount of progress has been made on the physical layer of computers, including the invention of the transistor in 1947 by William Shockley and his colleagues at Bell Labs. Transistors are dramatically improved versions of Shannon’s electrical relays — the best known way to physically encode Boolean operations. Over the next 70 years, the semiconductor industry packed more and more transistors into smaller spaces. A 2016 iPhone has about 3.3 billion transistors, each one a “relay switch” like those pictured in Shannon’s diagrams.
While Shannon showed how to map logic onto the physical world, Turing showed how to design computers in the language of mathematical logic. When Turing wrote his paper, in 1936, he was trying to solve “the decision problem,” first identified by the mathematician David Hilbert, who asked whether there was an algorithm that could determine whether an arbitrary mathematical statement is true or false. In contrast to Shannon’s paper, Turing’s paper is highly technical. Its primary historical significance lies not in its answer to the decision problem, but in the template for computer design it provided along the way.
Turing was working in a tradition stretching back to Gottfried Leibniz, the philosophical giant who developed calculus independently of Newton. Among Leibniz’s many contributions to modern thought, one of the most intriguing was the idea of a new language he called the “universal characteristic” that, he imagined, could represent all possible mathematical and scientific knowledge. Inspired in part by the 13th-century religious philosopher Ramon Llull, Leibniz postulated that the language would be ideographic like Egyptian hieroglyphics, except characters would correspond to “atomic” concepts of math and science. He argued this language would give humankind an “instrument” that could enhance human reason “to a far greater extent than optical instruments” like the microscope and telescope.
He also imagined a machine that could process the language, which he called the calculus ratiocinator.
If controversies were to arise, there would be no more need of disputation between two philosophers than between two accountants. For it would suffice to take their pencils in their hands, and say to each other: Calculemus — Let us calculate.
Leibniz didn’t get the opportunity to develop his universal language or the corresponding machine (although he did invent a relatively simple calculating machine, the stepped reckoner). The first credible attempt to realize Leibniz’s dream came in 1879, when the German philosopher Gottlob Frege published his landmark logic treatise Begriffsschrift. Inspired by Boole’s attempt to improve Aristotle’s logic, Frege developed a much more advanced logical system. The logic taught in philosophy and computer-science classes today — first-order or predicate logic — is only a slight modification of Frege’s system.
Frege is generally considered one of the most important philosophers of the 19th century. Among other things, he is credited with catalyzing what noted philosopher Richard Rorty called the “linguistic turn” in philosophy. As Enlightenment philosophy was obsessed with questions of knowledge, philosophy after Frege became obsessed with questions of language. His disciples included two of the most important philosophers of the 20th century — Bertrand Russell and Ludwig Wittgenstein.
The major innovation of Frege’s logic is that it much more accurately represented the logical structure of ordinary language. Among other things, Frege was the first to use quantifiers (“for every,” “there exists”) and to separate objects from predicates. He was also the first to develop what today are fundamental concepts in computer science like recursive functions and variables with scope and binding.
Frege’s formal language — what he called his “concept-script” — is made up of meaningless symbols that are manipulated by well-defined rules. The language is only given meaning by an interpretation, which is specified separately (this distinction would later come to be called syntax versus semantics). This turned logic into what the eminent computer scientists Allan Newell and Herbert Simon called “the symbol game,” “played with meaningless tokens according to certain purely syntactic rules.”
All meaning had been purged. One had a mechanical system about which various things could be proved. Thus progress was first made by walking away from all that seemed relevant to meaning and human symbols.
As Bertrand Russell famously quipped: “Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true.”
An unexpected consequence of Frege’s work was the discovery of weaknesses in the foundations of mathematics. For example, Euclid’s Elements — considered the gold standard of logical rigor for thousands of years — turned out to be full of logical mistakes. Because Euclid used ordinary words like “line” and “point,” he — and centuries of readers — deceived themselves into making assumptions about sentences that contained those words. To give one relatively simple example, in ordinary usage, the word “line” implies that if you are given three distinct points on a line, one point must be between the other two. But when you define “line” using formal logic, it turns out “between-ness” also needs to be defined — something Euclid overlooked. Formal logic makes gaps like this easy to spot.
This realization created a crisis in the foundation of mathematics. If the Elements — the bible of mathematics — contained logical mistakes, what other fields of mathematics did too? What about sciences like physics that were built on top of mathematics?
The good news is that the same logical methods used to uncover these errors could also be used to correct them. Mathematicians started rebuilding the foundations of mathematics from the bottom up. In 1889, Giuseppe Peano developed axioms for arithmetic, and in 1899, David Hilbert did the same for geometry. Hilbert also outlined a program to formalize the remainder of mathematics, with specific requirements that any such attempt should satisfy, including:
- Completeness: There should be a proof that all true mathematical statements can be proved in the formal system.
- Decidability: There should be an algorithm for deciding the truth or falsity of any mathematical statement. (This is the “Entscheidungsproblem” or “decision problem” referenced in Turing’s paper.)
Rebuilding mathematics in a way that satisfied these requirements became known as Hilbert’s program. Up through the 1930s, this was the focus of a core group of logicians including Hilbert, Russell, Kurt Gödel, John Von Neumann, Alonzo Church, and, of course, Alan Turing.
“In science, novelty emerges only with difficulty.”
Hilbert’s program proceeded on at least two fronts. On the first front, logicians created logical systems that tried to prove Hilbert’s requirements either satisfiable or not.
On the second front, mathematicians used logical concepts to rebuild classical mathematics. For example, Peano’s system for arithmetic starts with a simple function called the successor function which increases any number by one. He uses the successor function to recursively define addition, uses addition to recursively define multiplication, and so on, until all the operations of number theory are defined. He then uses those definitions, along with formal logic, to prove theorems about arithmetic.
The historian Thomas Kuhn once observed that “in science, novelty emerges only with difficulty.” Logic in the era of Hilbert’s program was a tumultuous process of creation and destruction. One logician would build up an elaborate system and another would tear it down.
The favored tool of destruction was the construction of self-referential, paradoxical statements that showed the axioms from which they were derived to be inconsistent. A simple form of this “liar’s paradox” is the sentence:
This sentence is false.
If it is true then it is false, and if it is false then it is true, leading to an endless loop of self-contradiction.
Russell made the first notable use of the liar’s paradox in mathematical logic. He showed that Frege’s system allowed self-contradicting sets to be derived:
Let R be the set of all sets that are not members of themselves. If R is not a member of itself, then its definition dictates that it must contain itself, and if it contains itself, then it contradicts its own definition as the set of all sets that are not members of themselves.
This became known as Russell’s paradox and was seen as a serious flaw in Frege’s achievement. (Frege himself was shocked by this discovery. He replied to Russell: “Your discovery of the contradiction caused me the greatest surprise and, I would almost say, consternation, since it has shaken the basis on which I intended to build my arithmetic.”)
Russell and his colleague Alfred North Whitehead put forth the most ambitious attempt to complete Hilbert’s program with the Principia Mathematica, published in three volumes between 1910 and 1913. The Principia’s method was so detailed that it took over 300 pages to get to the proof that 1+1=2.
Russell and Whitehead tried to resolve Frege’s paradox by introducing what they called type theory. The idea was to partition formal languages into multiple levels or types. Each level could make reference to levels below, but not to their own or higher levels. This resolved self-referential paradoxes by, in effect, banning self-reference. (This solution was not popular with logicians, but it did influence computer science — most modern computer languages have features inspired by type theory.)
Self-referential paradoxes ultimately showed that Hilbert’s program could never be successful. The first blow came in 1931, when Gödel published his now famous incompleteness theorem, which proved that any consistent logical system powerful enough to encompass arithmetic must also contain statements that are true but cannot be proven to be true. (Gödel’s incompleteness theorem is one of the few logical results that has been broadly popularized, thanks to books like Gödel, Escher, Bach and The Emperor’s New Mind).
The final blow came when Turing and Alonzo Church independently proved that no algorithm could exist that determined whether an arbitrary mathematical statement was true or false. (Church did this by inventing an entirely different system called the lambda calculus, which would later inspire computer languages like Lisp.) The answer to the decision problem was negative.
Turing’s key insight came in the first section of his famous 1936 paper, “On Computable Numbers, With an Application to the Entscheidungsproblem.” In order to rigorously formulate the decision problem (the “Entscheidungsproblem”), Turing first created a mathematical model of what it means to be a computer (today, machines that fit this model are known as “universal Turing machines”). As the logician Martin Davis describes it:
Turing knew that an algorithm is typically specified by a list of rules that a person can follow in a precise mechanical manner, like a recipe in a cookbook. He was able to show that such a person could be limited to a few extremely simple basic actions without changing the final outcome of the computation.Then, by proving that no machine performing only those basic actions could determine whether or not a given proposed conclusion follows from given premises using Frege’s rules, he was able to conclude that no algorithm for the Entscheidungsproblem exists.
As a byproduct, he found a mathematical model of an all-purpose computing machine.
Next, Turing showed how a program could be stored inside a computer alongside the data upon which it operates. In today’s vocabulary, we’d say that he invented the “stored-program” architecture that underlies most modern computers:
Before Turing, the general supposition was that in dealing with such machines the three categories — machine, program, and data — were entirely separate entities. The machine was a physical object; today we would call it hardware. The program was the plan for doing a computation, perhaps embodied in punched cards or connections of cables in a plugboard. Finally, the data was the numerical input. Turing’s universal machine showed that the distinctness of these three categories is an illusion.
This was the first rigorous demonstration that any computing logic that could be encoded in hardware could also be encoded in software. The architecture Turing described was later dubbed the “Von Neumann architecture” — but modern historians generally agree it came from Turing, as, apparently, did Von Neumann himself.
Although, on a technical level, Hilbert’s program was a failure, the efforts along the way demonstrated that large swaths of mathematics could be constructed from logic. And after Shannon and Turing’s insights — showing the connections between electronics, logic and computing — it was now possible to export this new conceptual machinery over to computer design.
During World War II, this theoretical work was put into practice, when government labs conscripted a number of elite logicians. Von Neumann joined the atomic bomb project at Los Alamos, where he worked on computer design to support physics research. In 1945, he wrote the specification of the EDVAC — the first stored-program, logic-based computer — which is generally considered the definitive source guide for modern computer design.
Turing joined a secret unit at Bletchley Park, northwest of London, where he helped design computers that were instrumental in breaking German codes. His most enduring contribution to practical computer design was his specification of the ACE, or Automatic Computing Engine.
As the first computers to be based on Boolean logic and stored-program architectures, the ACE and the EDVAC were similar in many ways. But they also had interesting differences, some of which foreshadowed modern debates in computer design. Von Neumann’s favored designs were similar to modern CISC (“complex”) processors, baking rich functionality into hardware. Turing’s design was more like modern RISC (“reduced”) processors, minimizing hardware complexity and pushing more work to software.
Von Neumann thought computer programming would be a tedious, clerical job. Turing, by contrast, said computer programming “should be very fascinating. There need be no real danger of it ever becoming a drudge, for any processes that are quite mechanical may be turned over to the machine itself.”
Since the 1940s, computer programming has become significantly more sophisticated. One thing that hasn’t changed is that it still primarily consists of programmers specifying rules for computers to follow. In philosophical terms, we’d say that computer programming has followed in the tradition of deductive logic, the branch of logic discussed above, which deals with the manipulation of symbols according to formal rules.
In the past decade or so, programming has started to change with the growing popularity of machine learning, which involves creating frameworks for machines to learn via statistical inference. This has brought programming closer to the other main branch of logic, inductive logic, which deals with inferring rules from specific instances.
Today’s most promising machine learning techniques use neural networks, which were first invented in 1940s by Warren McCulloch and Walter Pitts, whose idea was to develop a calculus for neurons that could, like Boolean logic, be used to construct computer circuits. Neural networks remained esoteric until decades later when they were combined with statistical techniques, which allowed them to improve as they were fed more data. Recently, as computers have become increasingly adept at handling large data sets, these techniques have produced remarkable results. Programming in the future will likely mean exposing neural networks to the world and letting them learn.
This would be a fitting second act to the story of computers. Logic began as a way to understand the laws of thought. It then helped create machines that could reason according to the rules of deductive logic. Today, deductive and inductive logic are being combined to create machines that both reason and learn. What began, in Boole’s words, with an investigation “concerning the nature and constitution of the human mind,” could result in the creation of new minds — artificial minds — that might someday match or even exceed our own.
This piece first appeared in The Atlantic.





